MasterSeries Blog
How can we determine the sensitivity of a steel frame to second-order effects to Eurocode?
According to Eurocode 3, if the deformed geometry significantly modifies the structural behaviour we have to take into account the influence of the deformation in the analysis. But how can we determine that our structure is sensitive for deformation or not and if it is how can we take into account during the analysis?
The Eurocode EN 1993-1-1, section 5.2.1 (3) defines the following criterion which helps to determine the behaviour of our structure.

So the sensitivity to effects of deformed geometry is measured by the critical load factor (αcr).
The critical load factor (and the corresponding mode shapes) can be determined by calculation software which is able to carry out elastic buckling analysis. In this case, we have to look through the calculated buckling modes and find graphically the first swaying mode of the structure. The first swaying buckling mode provides us the relevant critical load factor to decide whether or not our structure is sensitive to second-order effect and second-order analysis is needed or not.
Alternatively, the Eurocode EN 1993-1-1, section 5.2.1 provides us a simplified calculation method for buildings (portal frames with shallow roof slopes and beam-and-column type plane frames in buildings). The above criteria must be satisfied for each storey.
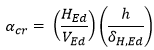
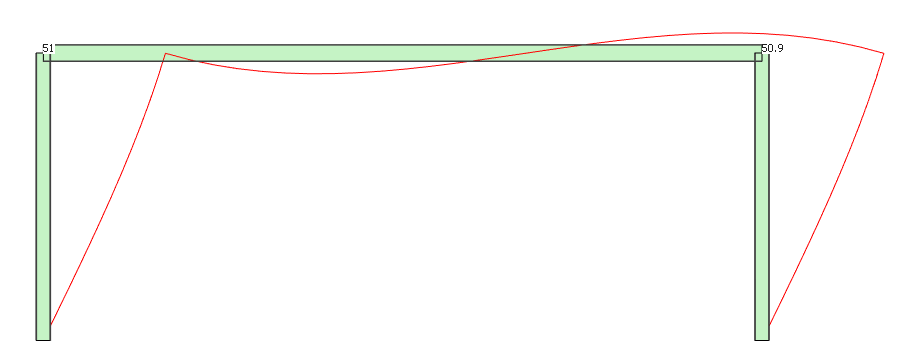
where, HEd is the total design horizontal load
VEd is the total design vertical load
δH,Ed is the horizontal displacement at the top of the storey, relative to the bottom of the storey
h is the storey height In our example, we have a goal post with the following dimensions. The columns are pinned on the bottom and rigidly connected to the beam.
In our example, we have a goal post with the following dimensions. The columns are pinned on the bottom and rigidly connected to the beam. The vertical loading is two -50 kN nodal loads on the top of the columns and we have 20 kN horizontal load on the top of the left column.

Analysing the frame to first-order we get a 50.9 mm horizontal top displacement.
Using the Eurocode simplified critical load factor method, we get the following critical load factor (αcr):
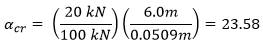
Since the calculated critical load factor is greater than 10, therefore, according to the Eurocode 3 rules, our sample frame is not sensitive to the second-order effects. The second-order analysis is not required.
Calculating the same frame in MasterSeries we get the same αcr value.

Explore how MasterSeries can help you design more economical solutions and boost your productivity.
Try it for yourself with a free 14-day trial.
Categories
- About
- Beam Designer
- BIM
- Composite design
- Concrete Design
- Connections
- Dynamic
- Educational
- General
- LCA
- Masonry
- MasterFrame
- Pile Cap
- Portals
- PowerPad
- Retaining wall
- Steel Design
- Webinar
- Wind Analysis
