MasterSeries Blog

Concrete structures experience creep and shrinkage strains, which increase over time. Further more the concrete material may experience cracking, leading to reduction in stiffness. All these factors will affect the in-service deflection behaviour, but how can we take it into consideration in our design?

The common method is to take into account the estimated effects of cracking, creep and shrinkage in long-term deflection calculations by using a reduced Young’s modulus. However, for rigorous deflection calculation of concrete elements, it is necessary to use an analysis that automatically determines and modifies the material properties to account for the age of the concrete at the time of loading.

Creep

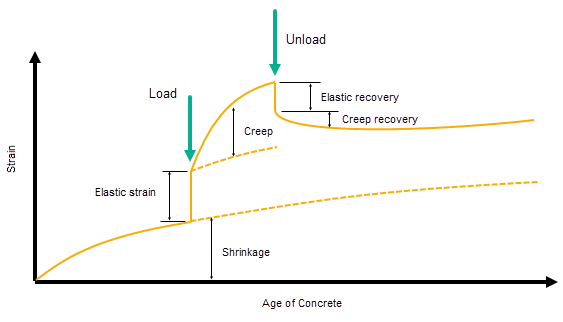
Creep is the tendency for a material to undergo continuous and permanent deformation under conditions of permanent stress, even in cases where the stress is significantly less than the yield stress of the material. Therefore, creep causes an increase in strain, but without a corresponding change in stress. Creep strains can be significant and so the influence of creep on the long-term deformation of the structure can also be significant.

In concrete elements such as beams and slabs, under bending the resulting stress condition is such that there are clearly defined compression and tension regions in the slab, creep leads to additional strain in the compression zone of the element, which is turn results in additional deflections of the structural element.

Since creep is associated with increased strain but without a change in the stress over time, then this results in a modification in the Elastic modulus of the material over time, since Young’s modulus (E) is given by:

Thus, in concrete, the elastic modulus is also a time-dependent property of the material, with a decrease over time associated with creep of the material. However, concrete also gains strength over time due to the curing process, which sees an increase in the elastic modulus over time. Both the British Standard and Eurocodes use an effective elastic modulus to account for the time-dependent nature of the Young’s modulus, utilising a creep coefficient to modify the short-term Elastic modulus. The effective modulus is given by:

were

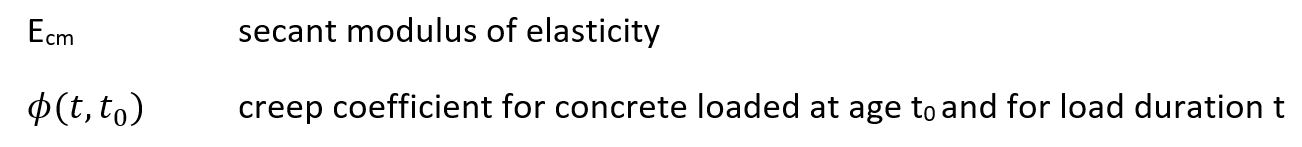
The main parameters which affect the creep of the concrete are:

• the mean compressive strength of the concrete
• the age at loading
• the cement type
• the relative humidity
• the duration of loading
• the cross-sectional area and exposed perimeter of the section
• temperature
• stress limitation

Shrinkage

Shrinkage of concrete changes the volume of concrete which results in additional strain. The change in volume results from the loss of moisture during the curing and drying process. The amount of drying shrinkage that occurs in concrete structures depends on the constituent materials that make up the concrete, the proportions of the constituent materials, how the concrete is cured, environmental factors such as humidity and temperature and the degree of restraint to the structure.

When calculating the shrinkage, the following factors are taken into consideration in the equations:

• cement type
• water/cement ratio
• aggregate type
• age at exposure
• surface area exposed
• member size and shape
• reinforcement quantities and position
• relative humidity
• curing

Shrinkage is made up of two components, drying shrinkage and autogenous shrinkage.

Drying shrinkage

Drying shrinkage occurs due to the loss of water by capillary action. This leads to a compressive stress on the concrete which results in a contraction or loss of volume over time, resulting in the contraction of the concrete and subsequent strain. Since the migration of water through the hardened concrete is slow, drying shrinkage occurs over an extended period of time and so is a gradual but long-term effect. Structural elements which have a large surface area relative to their volume will undergo a more significant loss of water and so have higher subsequent drying shrinkage. Where the structural elements have a high degree of restraint, more cracking will develop as a result of the drying shrinkage.

Drying shrinkage is the main cause of shrinkage in the concrete and occurs throughout the life of the concrete.

Autogenous shrinkage

Autogenous shrinkage occurs in early age concrete and is the result of pore water being drawn into the hydration process. As water is drawn in, the demand for more water results in fine capillaries being created in the concrete matrix. The surface tension within the capillaries results in a compressive stress in the concrete and a resulting strain and the formation of cracking.
Autogenous shrinkage tends to be significant in elements that have small cross-sections and/or low water/cement ratios. Since it is linked to the hardening of the concrete, the majority of the autogenous shrinkage tends to occur early in the life of the concrete.

Predicting shrinkage

BS 8110-2 provides a method for predicting the effects of drying shrinkage at 6 months using a chart as given in Figure 7.2, Section 7. The range of applicability of this method is limited since it requires a limited range of values based on an assumed water content and assumed aggregate types. Figure 7.2 does not lend itself to automated calculation within software. However, similar predictions of drying shrinkage can be achieved using BS 5400-4.
EC2 provides a tabular method for estimating drying shrinkage in Table 3.2 of Section 3.1.4. However, a method to calculate the drying shrinkage is given in Appendix B.2 which, when combined with Clause 3.1.4(6) provides a method to estimate the strains due to drying and autogenous shrinkage.

Deflection

Once the creep and shrinkage effects have been calculated, their effects on the deflections of the slab have to include in the deflection calculation. Within the FE analysis, this requires the modification of the material factors to account for creep and a subsequent modification of the curvature of the section due to shrinkage, but other factors must also be considered as part of the analysis. These factors include the tensile strength and its variation with time, the loading at relevant time intervals, and the extent of cracking over time which will modify the cross-sectional properties and so affect the stiffness of the structure.

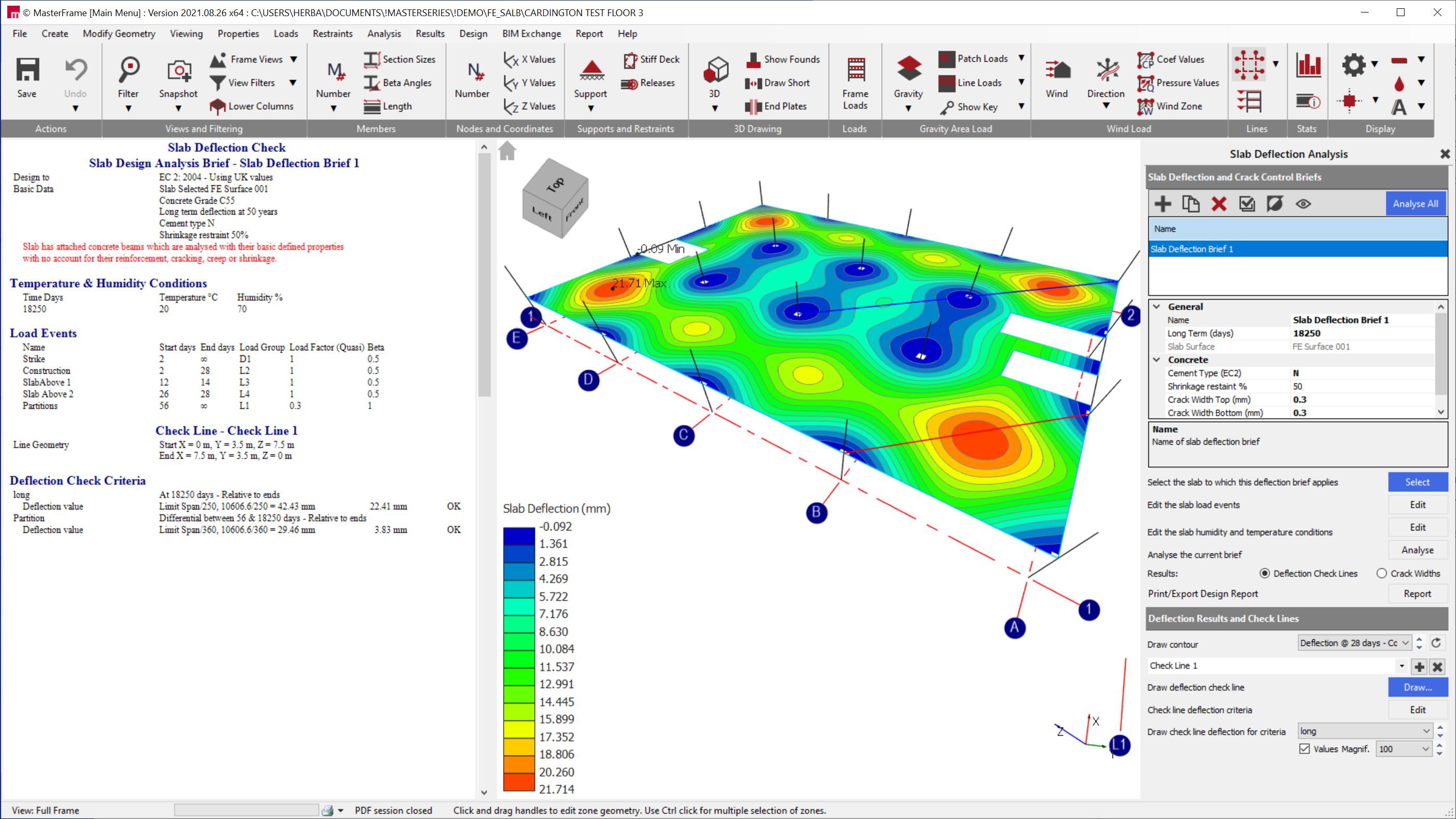
Calculating long-term deflection and crack width for concrete slabs [WEBINAR]

In our upcoming webinar, our lead developer, Dr Martin O'Gara will talk in detail about all aspects of the long-term deflection calculation and show you how you can calculate it using the MasterSeries.

Date: Wed, 15th September 2021
Time: 1:00 PM - 2:00 PM BST