MasterSeries Blog

The process of producing a model requires that the structure is idealised into a suitable form for modelling. This often requires at least some degree of simplification. Such a process of simplification applies not just to the model geometry itself, but also to the loading and restraint conditions. In some circumstances, such simplification can be done in a variety of ways with no significant impact on the overall analysis, but there are cases where how the loads or restraints are modelled can have a significant effect on the results.

Author: Barry Millar (Technical Support Engineer)

Saint Venant’s Principle

In 1855, Adhémar Jean Claude Barré de Saint-Venant, a French mathematician and scientist, stated the following principle:

“If the forces acting on a small portion of the surface of an elastic body are replaced by another statically equivalent system of forces acting on the same portion of the surface, this redistribution of loading produces substantial changes in the stresses locally, but has a negligible effect on the stresses at distances which are large in comparison with the linear dimensions of the surface on which the forces are changed.”

Saint Venant’s principle allows structures to be modelled using idealisations of loadings and restraints without a change in the overall forces and stresses, even though locally the stress distributions can be significantly different. This allows loads to be idealised and applied as point loads or uniformly distributed loads even though neither, particularly point loads, actually occur in reality; loads are applied over areas, not at specific points or on lines with length but no width. Saint Venant’s principle also applies to the idealisation of support conditions, particularly when modelled as nodal restraints.

An example – a member in axial tension

Consider a member of uniform cross section, with no holes, in pure axial tension.

The stress in the member is taken to be

The design codes require that the cross-section capacity, calculated in terms of force, is greater than the applied tensile load. In stress terms, the applied stress must be less than the allowable stress. No explicit mention of how the forces are applied is made in the analysis, and the design is based on the assumption of uniform stress.

The effect of the load application can be investigated in more detail by using a more refined finite element analysis. Consider two identical metal plates, positionally restrained at the left-hand edge with a statically equivalent tension load applied at the right-hand edge, one with a point load and the other with an equivalent line load. For the purposes of this analysis, the self-weight has been ignored so the only loading is due to the applied axial tensile force. The resulting stress from the FE analysis is shown below.

The application of a uniform linear load produces a uniform tensile stress in the bar. However, with the application of a point load, the vast majority of the plate is also in uniform tension, but there is a localised zone within which the stresses produced by the point load are significantly different from that produced by the uniformly distributed load. It can be seen, however, as per Saint Venant’s principle, that the localised stresses differ only over a small portion of the plate or bar. Far enough away from the application of the loading, the results are undisguisable.

More complex loading

Saint Venant’s principle is not restricted to simple loading cases, nor to tension loading. The following example provides three methods of modelling a triangular compression load on; a triangular linear load, an equivalent point load positioned at the centroid of the triangular load, and a centrally applied point load with additional point loads to produce a couple equal to that produced by the offset point load.

As per the first example, there is a short zone adjacent to where the loadings are applied, where the stresses produced by the different loadings are markedly different, but beyond this region the resulting stress distributions are the same.

The same effects are also found with out-of-plane loading as have been shown above with in-plane loading.

Restraint conditions

Saint Venant’s principle can be applied to the modelling of support and restraint conditions as well as for loadings. Hence, is it possible to model complex support conditions by means of a statically equivalent set of supports.

The following example represents a cantilevering plate with a vertical line load. The support conditions are modelled as a linear positional restraint or as a series of nodal restraints.

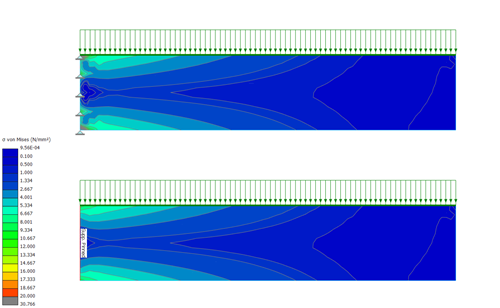
As before, close to the supported edge there is significantly variation in the results produced by the two models, but within a short distance the results of the analysis are again consistent.

FE surfaces, point load and restraint singularities

A common issue when dealing with the results of an FE analysis is interpreting the results near points of singularity, whether due to the application of loading as point loads, or due to restraint conditions from line elements (columns, beams etc) or nodal restraints. The issue of anomalous high stresses can, to some degree, be avoided by the use of patch loads instead of point loads, or by using a modified FE mesh by specifying stiff regions at column and/or wall interfaces. However, modelling point loads as patch loads can be time consuming while stiff regions necessarily complicate the meshing and can lead to difficulty achieving a valid mesh.

Saint Venant’s principle shows that the effect of the singularity is limited in its extent. The use of point loads rather than localised patch loading has no effect on the model results are you move a relatively small distance from the point of application of the load. The same effect can be seen for other singularities; the region over which the results are affected by the singularity is limited and the overall results are not influenced by the singularity. The design of the structural element at locations outside of the effect of the singularity can, therefore, be based on the FE results without significant concern and without the need to use more complicated load modelling and meshing.

The design of the region within the area affected by the singularity, however, will be heavily influenced by how the loading and restraint conditions are modelled, and how the element is going to be designed in these zones must be given consideration. An example of such a situation would be a transfer slab supporting a column above – modelling the column as a point load will give the correct overall results, but punching shear checks are needed on the slab to account for localised effects.

Limitations of Saint Venant’s principle – size effects and stiffness

Consider a model of a shear wall using FE surfaces. Frequently the support to the wall will be continuous and this can be modelled as a continuous FE edge restraint. However, applying Saint Venant’s principle, it is possible to restrain the base of the wall in a number of statically equivalent ways, as shown below.

Looking at the vertical stress in the three models, it can be seen that, as predicted by Saint Venant’s principle, the stress beyond a short zone around the supports gives effectively identical results.

However, when checking the lateral deflections of the structures, there are noticeable differences in the returned deflection values. A view at large scale at the base level of the three walls reveals significantly different strains and deflected shapes.

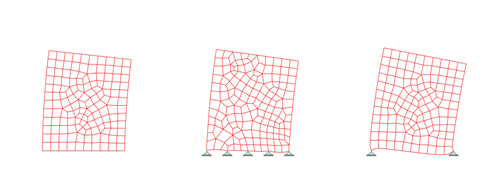
So, while the stress results are the same outside the zone of influence of the support conditions, the overall behaviour of the structural elements in terms of deflection do not show such close correlation. In other words, while the restraint conditions are equivalent from a stress perspective, and so any of the above are adequate for the structural design of the elements, the three models do not exhibit the same behaviour in terms of deflection.

The other issue with a cantilever wall with lateral loads is that the critical zone for the results is the base of the wall, and this is within the zone where the local stresses are affected by the variation of the restraint conditions. In this case, the restraint conditions need to be as close to the actual restrain conditions as can be achieved within the model.

Conclusion

Whether used consciously or not, engineers employ Saint Venant’s principle in most modelling and design scenarios to model real world situations using simplified, idealized loading and restraint conditions. But by being aware of the principle explicitly, it allows engineers to make informed choices to employ simplified loading and/or restraint conditions to simplify models, and yet retain their usefulness. This can be particularly helpful when it comes to linear elastic finite element analysis, where Saint Venant’s principle can be applied to simplify, or idealise, the model and yet retain confidence in the overall results, outside of reasonable small regions.

However, some care is needed since, for some models, it is not always the parts of the models that are far from the load or restraint condition that are of primary concern. In these cases, a more detailed analysis may be required to investigate the local effects and to ensure adequacy of the design.

Did you like this post? Don't miss similar topics!